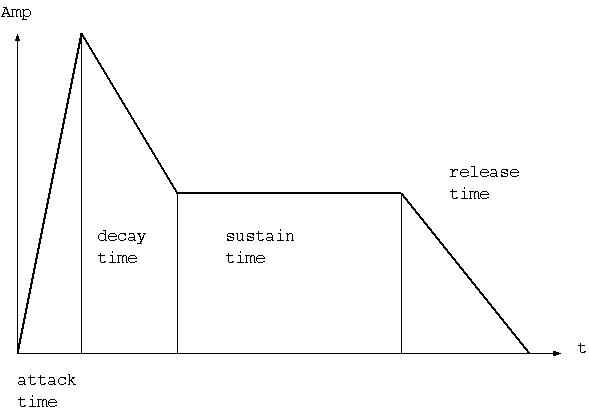
アタックタイムから、リリースタイムまで
また,研究の成果として,MATLABによる弦楽器のシミュレーションも行う.
ギターやピアノの場合,弦の振動が始まってから定常振動に移行する区間をアタッ
クタイムというが,これをコンピュータ上でシミュレーションすることで,
物理シミュレーションを利用した新たな方式のシンセサイザーを作り出すことが
できる.

アタックタイムから、リリースタイムまで
ピアノとギターのアタックタイムを入れ換え(アタックタイムのスワップ), 音色がどう変化するのかを検証する.また,アタックタイムのレベルの変化に対 して,人工的にエフェクトをかけて音色の変化を検証する. 検証の方法として,実際に複数の人にアンケートをとり, その結果から,アタックタイムが音色に相関があるのかを判定する. ピアノとギターは弦楽器である.これら二つの楽器の音色は,物理的には非常に 似通った振動をする. しかし,人間には簡単にギターの音とピアノの音を識別することができる. よって,音色の変化を人間の感覚で判定する方法が妥当である.
具体的には,複数の人にアタックタイムを除いた定常状態の音を聞かせ,
どれがギターでどれがピアノの音かを判定させる.
また,アタックタイムをスワップした音,人工的にアタックタイムにエフェクト
をかけた音も判定させる.
音階と鳴らす強さごとに,正解率を表にまとめ,アタックタイムの影響を検証す
る.
調査する項目を以下にまとめる.
弦は質量がほぼ均等に分布していると仮定し,その線密度をρ(kg/m)とする. また,自然長はLである. 弦は通常,横方向の曲げに対しての弾力と,縦方向の伸びにたいして弾力がある. 横方向に対する弾力をk_y,縦方向の弾力をk_xとする. また,空気抵抗によって減衰力が発生しており,その力は速度に比例すると仮定 して,その空気抵抗はCd(N/m/s)という比例定数で表すことにする. 弦の両端からは,張力T(N)がかかっており,その張力は弦のどの点に於いてもほ ぼ同じである.弦をN個の点の集まりと考え,各点に於いての座標と加速度を漸 化式で求めてゆく.
弦が振動している状態において, ある点P_n(x_n,y_n)から微小区間隔てた点を,点P_n+1(x_n+1,y_n+1)とする. 座標は,弦の両端の点を結ぶ直線をx軸,その直交軸をy軸としている.
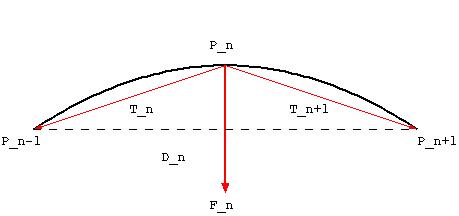
点P_nが両隣からの張力によって受ける力
点P_nにおける,隣り合う点からの張力の合力を,ベクトルF_nで表す. ベクトルF_nを成分表示すると
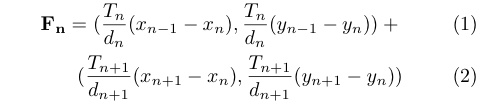
となる.ただしd_nとT_nは,
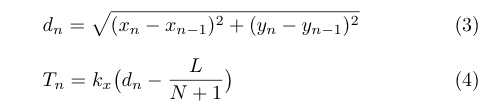
を満たすものとする.
正確なシミュレーションを実現するために,弦の曲げ剛性も考慮する.
曲げ剛性とは,弦が曲がることに対する弾性のことを指す.
このシミュレーションでは,「曲げに対する反発力は,描くカーブの直径に対して
単純に反比例する」と考える.
よって,ある連続した3点が作る三角形の外接円の半径を,順次求めてゆき,曲
げ剛性による力を計算する.
まず,P_nを中心とする3点の場合を考える.
ベクトルの内積から,
ベクトルのなす角を求める.
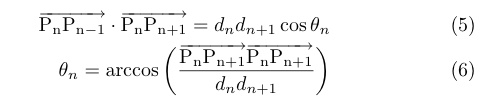
ここで,P_n-1とP_n+1の距離をD_nとおき,P_nを3点の中心として 考えた三角形の外接円の直径をR_nとおけば,

となる.
点P_nを中心に考え, 点P_nに於いての曲げ剛性による力をF'_nとおくと, 各3点に加わる力の大きさは,
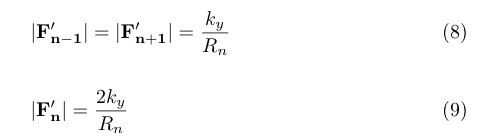
となる.
加速度は以下の式で表される.
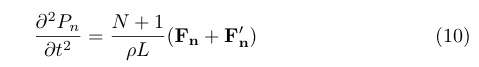
上で求めた加速度は,空気抵抗等を無視した場合の加速度であるが, 空気抵抗による減衰や,弦の伸びや曲げに対する弾力を考慮すると, より複雑な式となる.