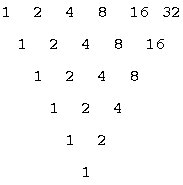math

連続量と離散量

★★”離散”とは？★★

人を数え上げる時、”1,2,3…”と、整数で数えていきますね。
１と２の間には1.5など無限に数があるにもかかわらず、数え上げるときはそれらの間にある数をとばしてしまいます。
このような”数え上げ”の量を”離散量”といいます。
”離散”とは”離ればなれ、とびとびの”という意味があります。
それに対して、”長さ”や”重さ”などの量を、”連続量”といいます。

★★次元は離散量ではない★★

０次元、１次元、２次元、３次元、４次元時空、
はては、４次元超空間などという言葉をよく耳にしますね。
でも、実は1.26次元なんてものも存在します。
これは”長さ（１次元）”と”面積（２次元）”の間にある物理量を指します。
こういった非整数次元はフラクタルと呼ばれる自己相似図形（拡大しても拡大してもきりが無いような図形）によく現れます。
もしも、この世界の素粒子がどんなに細かく分解しても果てがないとすれば、私たちの世界は3.33…次元とかになるかもしれませんね。 (実は９次元であるとする理論もあるようですが、詳しいことはわかりません）

★★弦のn倍振動★★

音楽で”オクターブ”という単位があります。
低い順に”ド、レ、ミ、ファ、ソ、ラ、シ、ド、レ……” と、続いていきますが、はじめのドと次のドは音階はあっていますが、周波数が二倍になっています。
このように周波数が二倍にあがることを音楽界では”１オクターブあがる” といいます。
また、２倍振動、３倍振動、４倍振動の時、良く調和するそうです……。
ところで、楽器類の音色を決めるのはn倍振動の各々の含有度で決まるといわれています。（基本振動音だけだと古代ファミコン音波になるようです）
ただし、”nは整数とする”！（笑

高等数学の離散数学

高等数学の中にも、いくつか離散的な考え方を要求される問題がありました。
例えば、（同様に確からしい場合においての）確率の問題です。
数学的確率は、”対象となる事象の数を、起こりうる全ての場合の数で割ったもの”です。
サイコロは１〜６までの目があり、それぞれの目が出る確率は同様に確からしいとします。
この条件で、２回ふって同じ目が二回連続出る確率は、

（対象となる事象）=(1,1)(2,2)(3,3)(4,4)(5,5)(6,6)の６つ

（全ての場合の数）=6×6で３６つ

よって、求める確率は、1/6となります。
確率自体は整数ではないのですが、 ”対象となる事象の数”と”全ての場合の数”は整数となります。
ほかにも、階乗の計算(!の記号)や、コンビネーション(nCmの記号)、パームテーション(nPmの記号)などは、離散数学の分野と言えるでしょう。

微分方程式とは？

★★空気抵抗は速度の二乗に比例する！★★

自由落下運動を、空気抵抗を考えなければ誰でも解けます。しかし、現実の世界で軌道計算をするとき、空気抵抗を無視すると大変な誤差が出ます。
空気抵抗の加速比率をkと置くと、自由落下運動の変位Xは、

X=∫(g-kvv)tdt

のようになりますが、右辺にvが入ってしまうため、高校レヴェルの微積では解くのは非常に困難ですね。
そこで活躍するのが微分方程式です。
速度は変位Xの時間に対する変化率であるため、dx/dtと書けます。
それによって、格段に解答が容易になるのです。

★★コーヒーの冷める速度は、温度差に比例する★★

気温２０の涼しい日。
今、９０℃の熱いコーヒーがあります。５分後には７０℃になりました。
では、１０分後には５０℃になるのでしょうか？
じつは、この考え方は全然違います。なぜなら、

冷却速度は、温度差に比例する

という、ニュートンの冷却法則なるものがあるからです。
冷却速度dx/dtは、温度差(X-20)に比例するから、比例定数をkとして、

dx/dt = k(x-20)　←両辺を(x-20)で割って、
dx/dt(x-20)^-1 = k

積分して、

∫(x-20)^-1dx/dtdt = ∫kdt
∫(x-20)^-1dx = ∫kdt

これを解くと、

log(x-20)+C = kt+C
よって、

ekt+c = x-20+...

実は、指数関数になるんですね。

★★無限階微分可能？★★

高等数学��までは、n次多項式の微分法だけを学びました。
数学��から、やっと無限階微分可能な関数の微分法を学びます。
微分を繰り返すということは、以下のようなことをいいます。
変位を時間で微分すると、速度になります。
速度を時間で微分すると、加速度になります。
加速度を時間で微分すると、加加速度になります。
加加速度を時間で微分すると、加加加速度になります。
加加加速度を（以下略）
のように、変化率の変化率の変化率の……と永久に続く関数は、無限階微分可能と言えます。
実生活でも無限階微分可能な現象は、預金利子率などに見られます。
簡単にするために、一年ごとに預金が２倍になる銀行があったとします。（あり得ない話ですが……）
一円預けたとして、一年後には２円になり、二年後には４円になり、三年後には８円、四年後には１６円、五年後には３２円になります。
以下に、その変化の様子を示します。

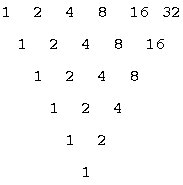
（上図のような解析を階差法といいます）
これは指数関数になるのですが、変化を見ると、１、２、４、８、１６、と、さらに指数関数になっていることに気付くと思います。
さらに、その変化の変化を見ると、１、２、４、８となっています。
また、それの変化は１、２、４となっています。
今回は五年後までの計算だったので五階目で微分不能（階差をとれなくなる）になりますが、関数自体は永久に微分できることが直感的に理解できたと思います。
さらに年数を増やして見ると、指数関数の数列が永久に現れることに気付きます。

近代の暗号化技術

★★8を25乗して、35で割ったあまりは？★★

ある人の解答：
”35は５×７、25は(5-1)×(7-1)+1、５と７は素数だから、
わかった！、こたえは８だ！”
度肝をぬく解答だが、事実です。
二つの任意の素数をそれぞれ、P,Qとすると、

Aのn×(P-1)×(Q-1)+1乗をP×Qで割った余りはAになる。(ただし、AはPQ以下、nは正の整数)

この数理の奇跡を利用したのが、今日の暗号化を担うRSA暗号なのです。

アルゴリズム体操

★★アルゴリズム=手続き★★

アルゴリズムとは、簡単に述べると”計算手順”のことです。
ただし、人間が行なう計算のようにアバウトな定義を許しません。
コンピュータに”お湯湧かして”と命令するには、命令が足りません。
”やかんに水を入れて、コンロの上に置いて、火をつけて、水が沸騰するまで待って、そしてコンロの火を消す。”などと命令してもまだまだ足りません。
コンピュータも数学者も、アバウトな定義を嫌います。（抽象的とは別）
よって、アルゴリズムは、だれが読んでも分かる手順（明確な定義）、どのような場合でも適用できること（一般性）、その方法が意味のあるもの（有用性）などの条件を満足できる計算手順が好ましいです。

カオス理論

★★チョウチョが羽ばたくとハリケーンが…？★★

”カオス(chaos)”を日本語で言うと、”混沌”と言う意味です。
数学的にほんの少しの誤差が予測もつかないほど影響し、結果が予測できないような現象のことをいいます。
例えば、もしもアインシュタインがナチスドイツ軍に殺害されたとしたら、歴史はどうなっていたでしょうか？
核兵器が無い世界になっていたかもしれないし、または何らかの原因で世界が崩壊していたかもしれません。もしくは何も変わらないかもしれませんね。
同じように、チョウチョの羽ばたきが極小の気圧の変化をおこし、その影響でハリケーンが起らないとも言い切れません（多少強引）
まさに、風が吹くと桶屋が儲かるようなものです(笑

★★カオスな関数の例★★

では、実際にカオスとはどのようなものかを可視化してみましょう。

数学トリビア集

★★ギャンブルの町モンテカルロ★★

サイコロを１回ふって、１の目が出る確率は？
と聞かれたら、普通は”対象となる場合の数/起こりうる全ての数”より、答えを1/6と導き出します。
ほかにも、実際に何回も振ってみて、統計から確率を出すのも１つの方法でしょう。
この後者の方法がモンテカルロ法です。
この方法を応用すれば、円周率をある程度正確に求めることが出来ます。
以下に一番簡単な方法を紹介します。
１辺が2センチの正方形の中に、半径１センチの円を描きます。
そうすると、

正方形全体の面積:円の面積

は、4:πになります。

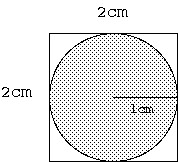
そこで、適当に正方形の中に沢山の点を打ちます。
点が円の内部に入る確率は、面積比よりπ/4となります。
この試行を繰り返し、点が円の中に入った割合を見れば円周率が求まりますね！
ちなみに、モナコ公国という小さな国に、モンテカルロというギャンブルの町があります。その地名が名前の由来です。
モンテカルロ法で円周率を求めるのは、一種のギャンブルのような気がしませんか？